Tutorials

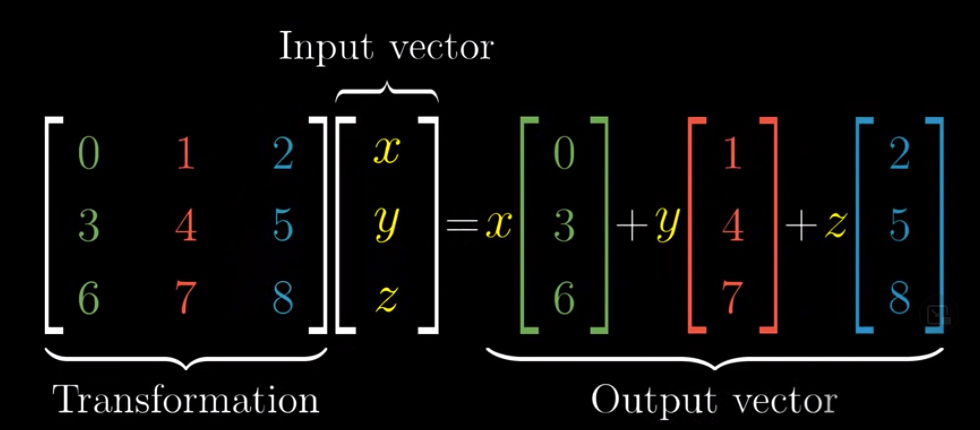
In machine learning, especially in linear regression, "solving for column coefficients" refers to finding the weights (coefficients) associated with each feature (or regressor) that best predict the target variable. Here’s a step-by-step explanation:

The Regression Model

• Model Equation:
  For a linear regression model, the relationship between the predictors X (a matrix of features) and the target y is modeled as: y=Xβ+ϵ where:
  • y is the vector of observed outcomes.
  • X is the matrix of input features (each column is a different feature).
  • $\beta$ is the vector of coefficients (one coefficient per feature).
  • ϵ is the error term.

Ordinary Least Squares (OLS) Solution

• Objective:
  The goal is to find the coefficient vector $\beta$ that minimizes the sum of the squared differences (residuals) between the observed values y and the predicted values Ŷ=Xβ.

• Solution Formula:
  The optimal coefficients can be computed analytically (when X^TX is invertible) as:

                                                   β = (X^TX)^-1 X^Ty

  This formula is derived by setting the derivative of the sum of squared errors with respect to β to zero.

Challenges and Enhancements

• Multicollinearity:
  If the features are highly correlated, X^TX may be nearly singular, making the inversion unstable. In these cases, regularization techniques like Ridge Regression (which adds an ℓ₂​ penalty) or Lasso Regression (which adds an ℓ_1​ penalty) can help stabilize the solution.

• Feature Selection:
  Not all columns (features) may be relevant. Techniques such as backward elimination, forward selection, or regularization (which can shrink some coefficients to zero in Lasso) help in selecting the right regressors.

4. Practical Considerations

• Scaling:
  Features are often standardized (e.g., z-score normalization) before solving for the coefficients to ensure that all features contribute equally.

• Iterative Methods:
  For very large datasets or complex models, iterative methods like gradient descent are used to approximate the coefficients rather than computing the closed-form solution.

Summary

Solving for the column coefficients in a regression problem means computing the values of $\beta$ that best fit your data. This involves setting up the model y=Xβ, minimizing the error (usually via least squares), and, if necessary, incorporating regularization or feature selection techniques to ensure a robust, interpretable model. These coefficients directly tell you how much each feature (column) influences the prediction, helping you identify the right regressors for your problem.